Zeno of Elea

Life and Work

Zeno (b. c. 490 BC) was a pupil of Parmenides. Plato in his dialogue Parmenides testifies their relationship. Aristotle names Zeno as the inventor of dialectic. He wrote a book in which he denies physical motion as well as the unreality of the pluralistic world. His paradoxes of motion had a great influence in the history and philosophy of mathematics.

Denial of Motion and Plurality

Zeno’s well known hypothesis is that of the denial of motion and plurality. His arguments aim to support Parmenides’ position on the oneness and unity of Being. For Zeno, if reality is successively divided into parts then you will divide it ad infinitum. Zeno’s arguments are presented in the form of paradoxes:

1.The Racetrack or Dichotomy Paradox

Suppose a runner has to travel form the start point A to the finish point B. But firstly he has to travel to the midpoint C and thence to B. But if D is the midpoint of AC, he must first travel to D and so on ad infinitum. So since in finite time it is impossible to accomplish an infinite number of movements then the runner is not able to finish his distance.

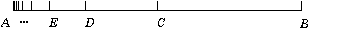
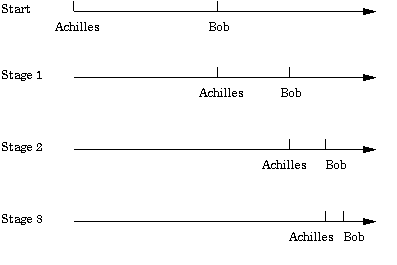
2.The Paradox of Achilles and the Tortoise

Achilles runs a race with a tortoise. Tortoise takes a lead. But while Achilles can run much faster than the tortoise, Achilles cannot touch it. How? When Achilles has reached the tortoise’s starting-point the tortoise is n/10 meters ahead. When Achilles has reached that point is n/100 ahead and so on ad infinitum.

3.The Stadium or Moving Blocks Paradox

Suppose three equal groups A, B, C of width l, with A and C moving past B in opposite direction at the same speed. While group A takes time t to traverse width B, it takes t/2 to traverse width C. This leads to the absurd paradox that half time equals its double.

4.The Arrow Paradox The Arrow Paradox

Suppose that time consists of moments or instances. A flying arrow at any instant of time occupies a space equal to itself. So at any instant of time, like in a photograph, the arrow would be at rest. Therefore if at any instant of time the arrow has no motion, temporal locomotion is impossible since time is composed of freezing instances in succession.

Fragments

Zeno's support of Parmenides: if there are many things then how many are they? (1), how big are they? (2), do they make a noise? (6), where are they? (4, 5) how can they move? (6)

1(3) how many? limited and unlimited in number

If there are many things (i) they will be just as many as they are, no more and no less; and if they are just as many as they are, they would be limited (in number).

If there are many things (ii) the things that there are are unlimited; for there will always be other things between the things that there are, and again other things between them, and so the things that there are are unlimited (in number).

2(1) how big? unlimited in size and no size at all

If what exists has no size (megethos) it would not exist. But if it does exist each thing must have some size (megethos) and thickness, and one part of it must be separate/distinct from another. And there is the same argument for what is in front, for that will have size and some part of it will be in front. Indeed, to say this once is similar to saying it for ever, for no such part of it will be the last or the same as a further part. So if there are many things they must be both small and great: so small as to have no size, and so big as to be unlimited (in size).

3(2) If it were added to something else, it would not make it any bigger; for if it has no size at all and were added on, it would not contribute any increase in size, and so what is now being added on would be nothing. And if, while it is being subtracted, the other will be no smaller It is obvious that what was added or subtracted was nothing.

4(4) where are they? in a place and nowhere at all

Where is all of what there is? if there is a place for the things that there are, where would it be? it would be in another place and that in another place and so on and so on. What moves does not move in the place in which it is or in the place in which it is not.

5(A24) If there is a place for the things that are, where would it be? it would be in another place and that in another place and so on and so on.

6(A29) do they make a noise? yes, some noise and no, no sound at all

Zeno: Tell me Protagoras, does a single millet seed make a noise as it falls, or does 1/10,000 of a millet? Protagoras: No.

Zeno: Does a bushel of millet seed make a noise as it falls, or not?

Protagoras: Yes, a bushel makes a noise.

Zeno: But isn't there a ratio (logos) between a bushel of millet seed, and one seed, and 1/10,000 of a seed? Protagoras: Yes, there is.

Zeno: So won't there be the same ratio of sounds between them, for the sounds are in proportion to what makes the sound? And if this is so, if the bushel of millet seed makes a noise so will a single seed and 1/10,000 of a seed.

7(A25-28 from Aristotle Physics 239b-240a) do things move? four puzzles

Zeno has four propositions (logoi) about movement which are puzzling for those who try to solve them:

(i) The Dichotomy (it is impossible to move from one place to another)

The first argument about there being no movement says that the moving object must first reach the half-way mark before the end (and the quarter-mark before the half and so back, so there is no first move; and the three-quarter mark after the half, and so forward so there is no last move).

(ii) The Achilles (Achilles cannot overtake the tortoise)

The second is the one called Achilles. This is it: the slowest will never be overtaken in running by the fastest, for the pursuer must always come to the point the pursued has left, so that the slower must always be some distance ahead.

(iii) The Arrow (the moving arrow is at rest)

The third one mentioned is that the moving arrow is at rest. [cf. Phys293b6: the arrow is at rest at any time when it occupies a space just its own length, and yet it is always moving at any time in its flight (i.e. in the 'now'), therefore the moving arrow is motionless.]

(iv) The Stadium (a time is twice itself)

The fourth is the one about equal blocks moving past equal blocks from opposite directions in the stadium - one set from the end of the stadium and one from the middle - at the same speed; here he thinks that half the time is equal to twice itself.

For example: AAAA are equal stationary blocks, BBBB, equal to them in number and size, are beginning from the half-way point (of the stadium), CCCC equal to these also in size, and equal to the Bs in speed, are coming towards them from the end. It happens of course that the first B reaches the end at the same time as the first C as they move past each other. And it happens that the C passes all the Bs but the Bs only half (the As) so the time is half (itself).

Translation M. R. Wright - note: numbers in parentheses refer to the standard Diels/Kranz order

Giannis Stamatellos

E-mail: gstamap@yahoo.com